Catalog

[数据结构复习] ZKW线段树

又是一年刷题/找实习/找全职的季节，虽然并不情愿，我也终于不得不投一些公司并且写一些算法题来热热手（其实我想的是好好做capstone/上OS呀），好在因为OI的经历，找回部分手感难度不大... 既然不算太忙，又鉴于博客已经断粮三个月，我就挑在做题过程中回忆起的数据结构中一些有趣的放在这里凑个数吧😳。

在各类算法题中，线段树是一个强大而十分好用的数据结构，能很好地解决动态接受单点修改而同时快速返回区间信息的需求。一个具体例子如下：

给定初始全为0的数组 [1,N]和一串操作：修改操作\((i, a_i)\)，将数组第\(i\)位元素被修改为\(a_i\)；查询操作\((a, b)\)，需要程序返回该区间内的最大元素

线段树可以在\(O(logN)\)的时间内完成每一个操作。线段树的原理和朴素实现并不是本文关注点，故不再赘述。需要指出的是，普通版线段树（即常规二叉树的构建、存储方式）存在如下问题：

内存访问局部性不强/缓存不友好：动态建树可能导致树上节点以离散的形式分布在内存中，该内存分布对连续树上访问不够缓存友好，从而导致一定程度地时间常数上升。该问题倒是可以通过一次性分配连续内存、并在该段内存中建树解决（给定N，需要的节点数是确定的）
递归建树，在一些边界情况可能比较error-prone。（嘛... 如果这种错误搞不定大概ZKW也啃不下来）
内存利用率偏低，假设64位运行环境，每个线段树节点存储左右子树指针，内部数据(payload)为一个32位整数，则内存利用率为\(\frac{32}{32+64*2}=20\%\)。尽管使用下标索引可以将利用率提高到\(33\%\)左右，但左右子树指针(或索引)这个压低利用率的元凶却依然无法解决。
操作常数较高：不管是单点修改操作还是区间查询操作都需要从线段树根进行一次递归访问，中间带来的压栈成本提高了整个过程的时间常数。

相比常规线段树，ZKW线段树则通过以下几个特性解决了上述缺陷：

强制连续存储：ZKW线段树强制存在连续的内存空间中(数组，vector等)，从而带来较好的局部性。
满二叉树型存储：通过类似二叉堆的索引方式存储整颗线段树，从而避免存储额外的左右子树指针/父节点指针等，从而节约了成吨的内存空间——ZKW的理论空间利用率极高，当N接近\(2^x\)(2的整数幂)时，空间利用率直逼\(100\%\)。
递推+位运算操作：任何操作都只需要一个while+若干位运算，常数极低。

说了这么多，现在开始具体讲一下ZKW线段树的实现。

前提条件

想拿到上述这么多优点并不容易，我们要解决的问题区间需要满足以下几个要求：

区间必须严格遵从 [1,n] (n>=1)的格式，任何不从 1开始的区间不满足要求。
\(n=2^x-2, x \in \mathbb{Z}\)

上述要求看起来苛刻，却不难从一般性问题转化而来：对于不从 1开始的区间，通过统一应用偏移量的方式调整至 1起始区间；对于n不满足要求的区间可以通过补充无用长度的方式补齐到最小的一个符合要求的值n'。

由于\(n' \geq n\)，空间利用率并不能达到理想的100%；但同时由于很容易证明得\(n'<2n\)，故空间利用率在最糟糕的情况下依然良好(50%)。同时我们也得出，当\(n\)趋向于\(n'\)时，空间利用率将接近完美。

索引方式 & 建树

如果对二叉堆有印象的读者不难想起，完全二叉树在内存中该如何编号能完全省略对指针的额外需求。ZKW线段树作为一棵满二叉树（特殊的完全二叉树）也是利用相同的索引方式来摆脱存储左右子树指针的空间开销。其内存分布如下：

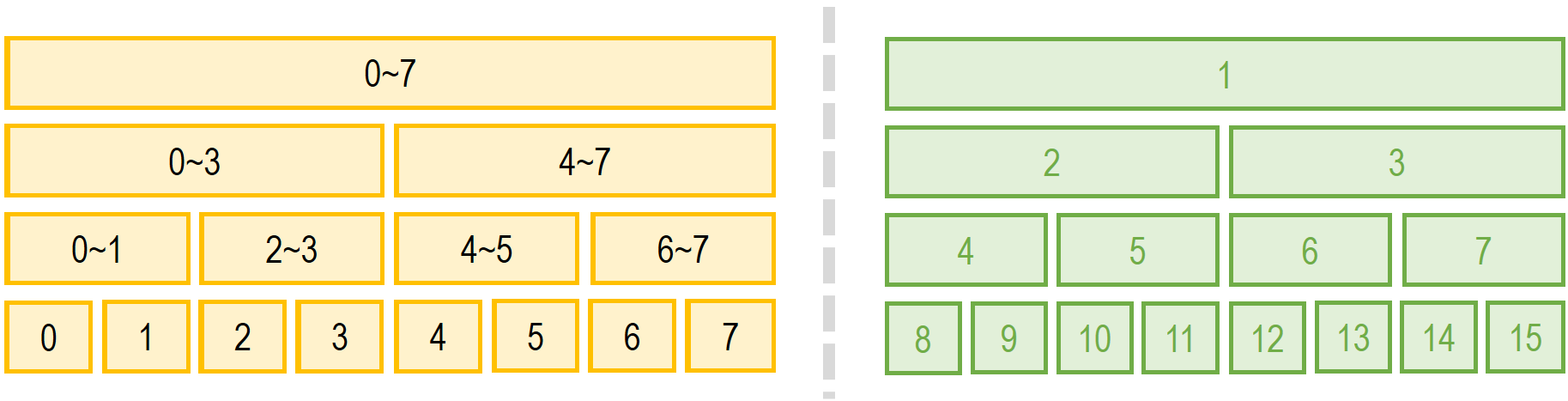
上图右边绿色部分表示该满二叉树每一个节点在数组中的索引，而左边黄色部分则表示对应节点所代表的区间范围。看到这里读者可能会疑惑：“不是强制 [1,n]么，不是\(n=2^x-2, x \in \mathbb{Z}\)么，这里的[0,7]完全没遵循这项准则呀。” 这个问题将在建树部分做解答。

建树

给定区间 [1,n]（满足上述条件），我们使用如下方式建树：

给区间补齐起始节点和结尾节点，使其成为 [0,n+1]。为何需要补充节点会在下文解释。
将上述n+2个节点放置于满二叉树的底层，由于\(n=2^x-2, x \in \mathbb{Z}\), 不难算出底层总元素个数为\(2^x\)，而这正是满二叉树的第\(x+1\)层。为了方便起见，我们定义\(\Sigma=2^x\)
根据上图的索引关系，底层元素 [0, n+1]分别对应着下标[\(\Sigma\), \(2 \cdot \Sigma-1\)]

故，建树过程仅仅两步：建立一个大小为\(2 \cdot \Sigma\)的数组、初始化即可:

auto zkwTree = std::vector<int>(2*sigma, 0);

单点修改

单点修改操作在ZKW线段树里非常直观，对于对点i的单点修改只需找到其索引并沿着满二叉树一路向上更新即可。例如，在 [1,6]区间生成的ZKW线段树上修改节点3的访问路径如下：

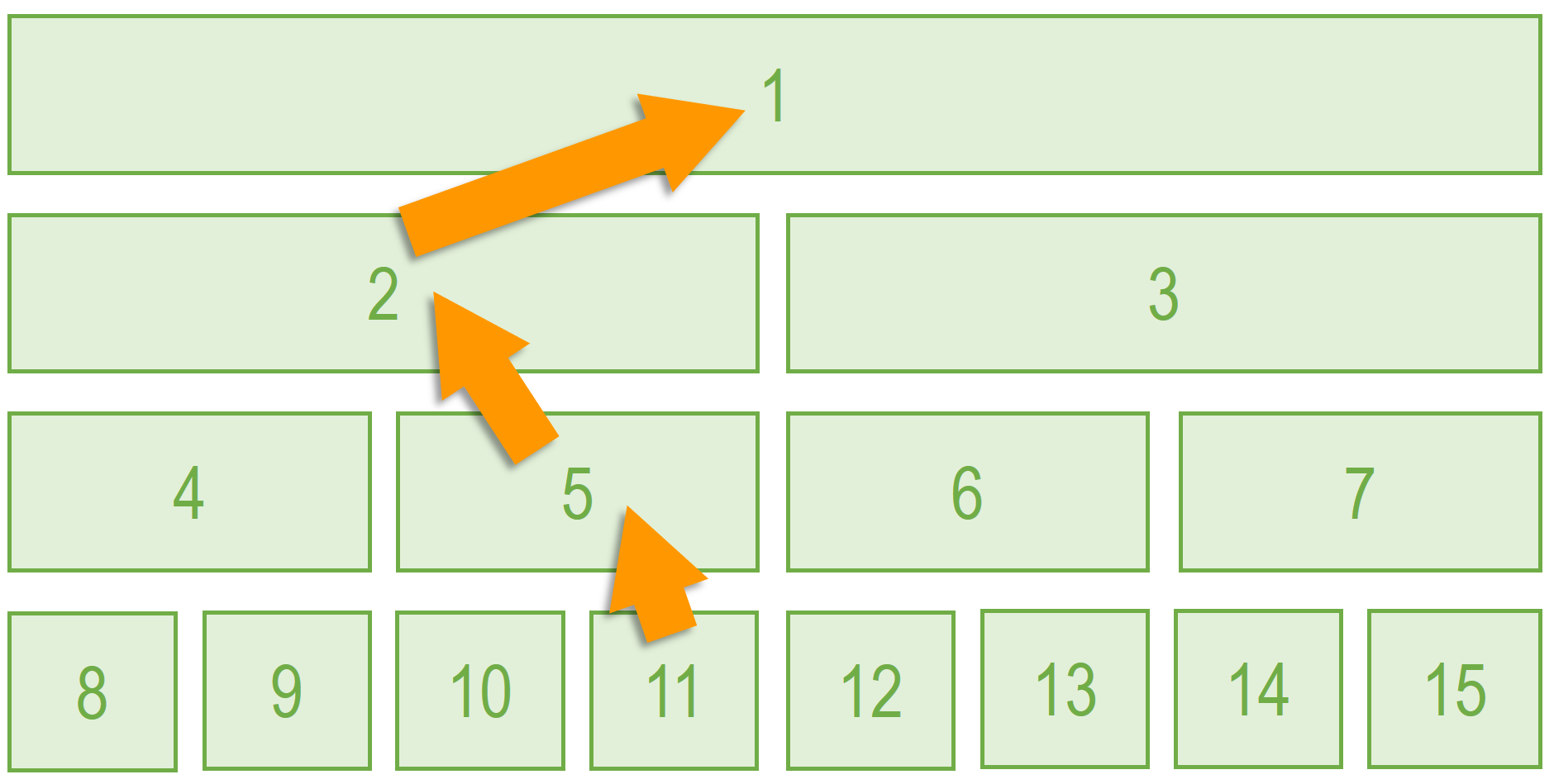
对应代码如下（依然使用区间最大值作为被维护的信息）

void update(const std::vector<int>& zkwTree, int position, int value) {
    position += sigma;
    while (position > 0) {
        zkwTree[position] = max(zkwTree[position], value);
        position >>= 1;
    }
}

区间查询

区间查询操作为整个ZKW线段树的精髓，对于其原理正确性的证明感兴趣的读者可以自行完成。本节将用例子和代码说明ZKW线段树区间查询的算法流程。

对于 [a,b]区间上的区间查询，我们需要首先将其修改为开区间 (a-1, b+1)进行树上操作。正是由于此处拓展区间的需求，我们才需要在建树时补充上 0号节点和 n+1号节点。对于开区间的两个端点 (a', b')，我们算出其所在的树上索引，并同时对两个点向父节点游走，直到两点间不存在任何其他节点。在游走过程中，任何有效点的数据将被记录从而生成最终查询结果。

有效点的定义为：左边界游走过程中的右兄弟（如果存在），以及右边界游走过程中的左兄弟节点（如果存在）。该定义过于抽象，故用下图补充：

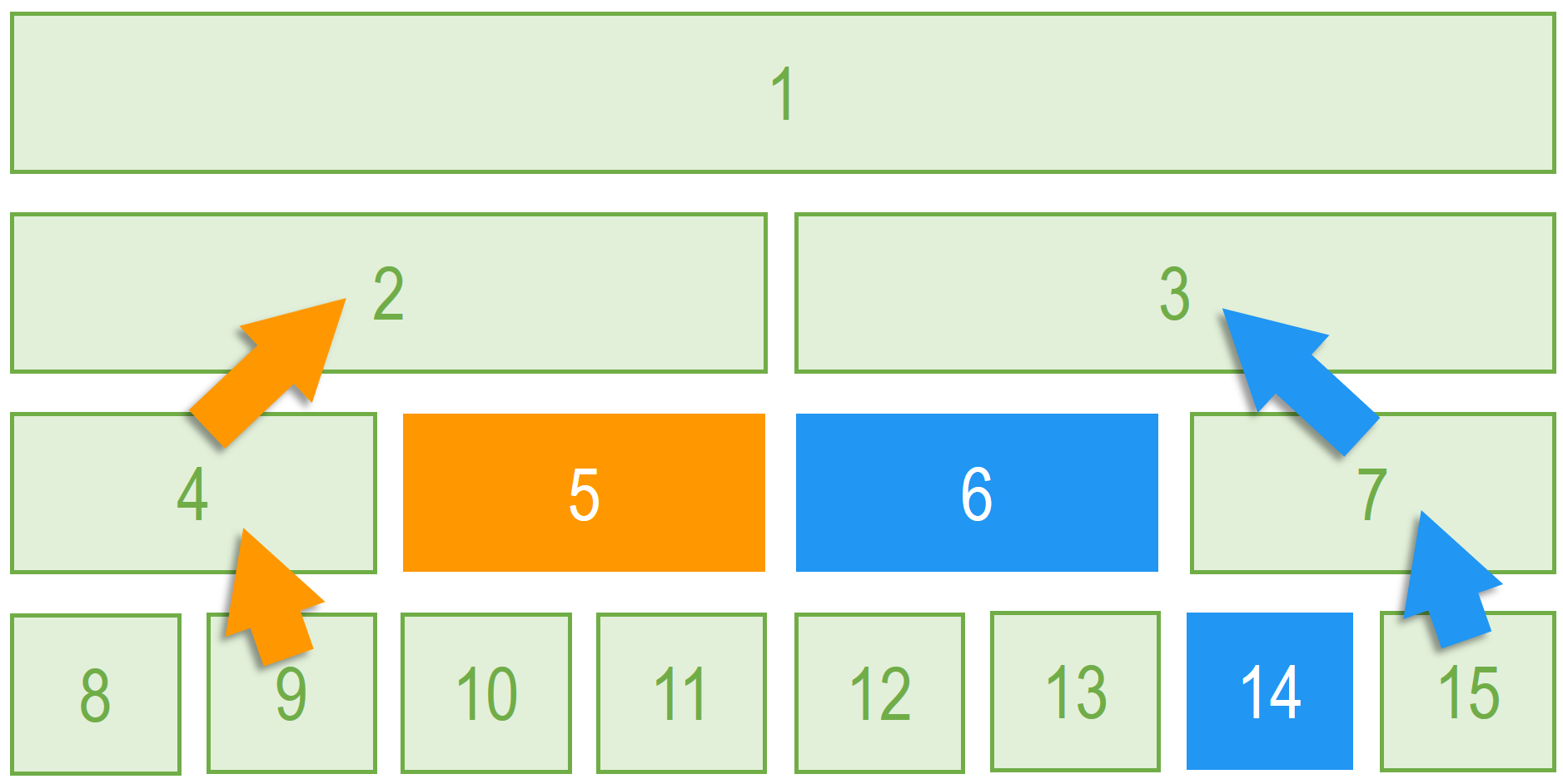
在该树上，我们需要查询区间 [2, 6]，通过拓展成开区间 (1, 7)并确定树上索引 (9, 15)，我们对左边界 9以及右边界 15进行游走。其中橙色箭头为左边界游走路线，蓝色箭头为右边界，而对应颜色的节点则是对应边界在游走过程中碰触到的有效节点。从该图上我们能直观得出，有效节点是在左右边界内，且父节点不再在左右边界内的节点。对于有效节点进行数据搜集，能保证区间被全部涵盖（完备性），但节点间表示的范围没有重合（互斥性），从而保证在正确前提下的最小访问次数。

将该流程体现在代码上如下，其中涉及到的位运算并不困难，请读者自行考虑各自目的：

int lookup(const std::vector<int>& zkwTree, int start, int end) {
    start += sigma - 1;
    end += sigma + 1;
    auto answer = 0;
    while (start < end-1) {
      if (start & 1 == 0) answer = max(answer, zkwTree[start ^ 1]);
      if (end & 1 == 1) answer = max(answer, zkwTree[end ^ 1]);
      start >>= 1;
      end >>= 1;
    }
    return answer;
}

总结

ZKW线段树凭借其极简洁的代码、干劲利落的操作、无懈可击的实际表现、~~超高的逼格~~成功把我发展为忠实拥趸。趁现在面试季刚好顺手分享出来，希望能获得更多人的认可。以上。